The first step in hanging a lighting truss is understanding the loads (weight and position) the truss
will be supporting. Fortunately, calculating lighting truss loads is really quite straight forward.
The diagrams on this page covers most of the situations commonly encounterd. The basic process is to compute the load for each hang
point for each load point, starting with uniformly distributed loads, then midspan loads, then any
cantilever loads, then sum them for each point. Once the hang point load is computed, multiply by
the load factor to size the hoisting load. Hoisting load is the total weight of the hoist, it's power
and control cables, spansets, shackles, burlaps, and steels. Finally add the hoisting load to get the
final hang point load. Consideration should be taken for socapex/dmx cables and whether those loads
are supported from the hang point (such as when these cables drop to the floor) or are separately
supported as when they are dropped from the grid above. Be careful that these loads are almost always
cantilever loads when dropped to the floor from the end of the truss.
Normally weight is computed in pounds or kilograms, lenths are coumputed in feet or meters. Always use the same unit of measure for all calculations.
As always, before suspending loads overhead consult a qualified engineer or rigger.
Normally weight is computed in pounds or kilograms, lenths are coumputed in feet or meters. Always use the same unit of measure for all calculations.
As always, before suspending loads overhead consult a qualified engineer or rigger.
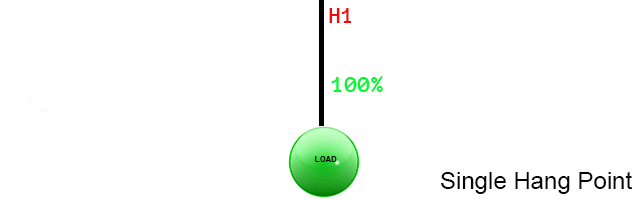
A speaker cabinet is an example of a single point load. In this case, the total weight of the cabinet,
it's hardware and cabling is figured at 100%.

An empty truss to be hung on two points is an example of an uniformly distributed load when all of the
weight is between the two points. Here the weight is evenly divided between the two points.


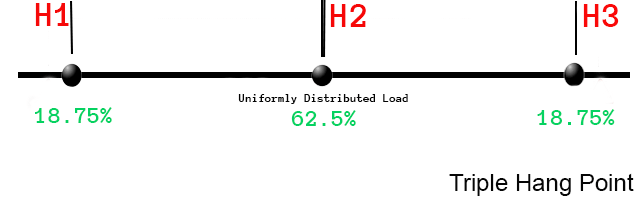
A uniformly distributed load on three points. When a third point is added, the center point carries over half of the load.

The general formula for computing point loads
where H1 = computed load on left point,
H2 = computed load on right point,
pl = the weight of the point load,
d1 = distance from pl to H1,
and d2 = distance from pl to H2.
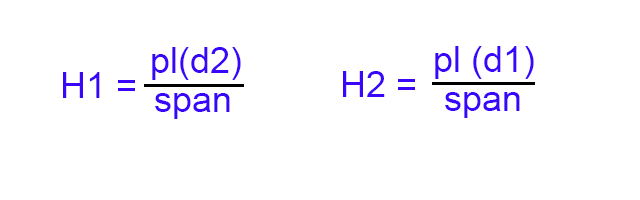 The following diagrams illustrate how the formula
applies to various load configurations:
The following diagrams illustrate how the formula
applies to various load configurations:
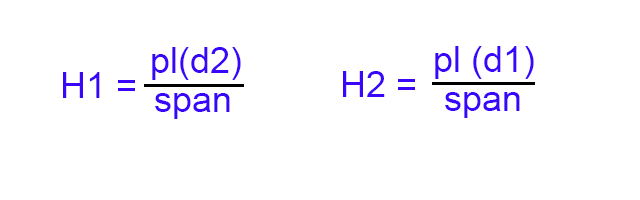
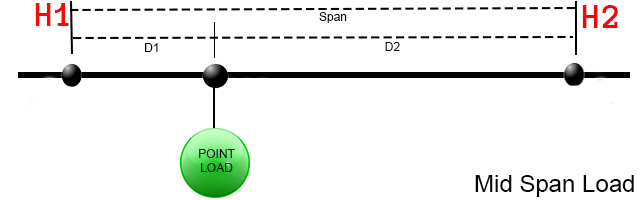
Point loads between two hang points. As the point load approaches a hanging point, the load on that point increases while
the load on the other point decreases proportionately. The computed H1 load is added to the near point and the computed H2
load is added to the far point.

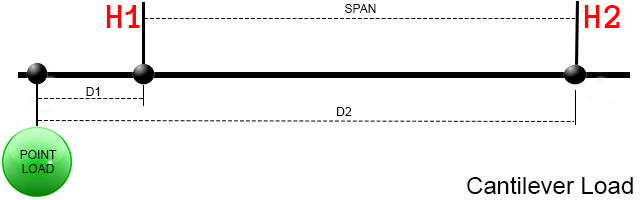
Cantilever point loads. When point loads are cantilevered, the net effect results in increased load
on the near point and reduced load on the far point. The computed H1 load is added to the near point and the computed H2
load is subtracted from the far point. However, where d1 is greater than span additional phantom load appears on
the near point and should generally be avoided.

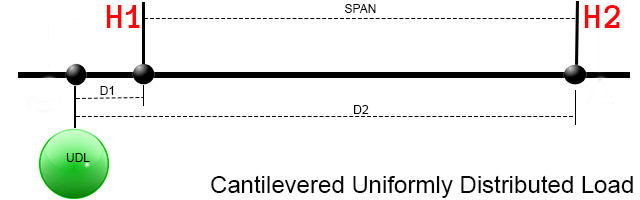
Uniformly distributed cantilever loads. When the cantilevered point load is uniformly distributed (say for example drapery), the
calculation is the same as cantilever point load however, you treat the total UDL as centered on a single point in the mid point of the
cantilever. The computed H1 load is added to the near point and the computed H2 load is subtracted from the far point.
However, where d1 is greater than span additional phantom load appears on
the near point and should generally be avoided.

Cite As:
Stagecraft Production Service. Lighting Truss Loading. https://bit.ly/2ZkAyvi
